Фэн-шуй во всех сферах жизни風水

Построение двух точек схода и линий высоты.

Две точки схода.

Давайте найдем и построим вторую точку схода для кирпича.

Положите этот кирпич на стол так, чтобы вам были видны три его стороны.

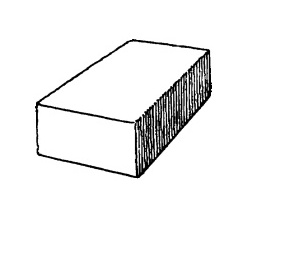
Рис. 5.1.

Теперь у нас есть три линии, которые можно продолжить, определив таким образом точку схода и уровень глаз.

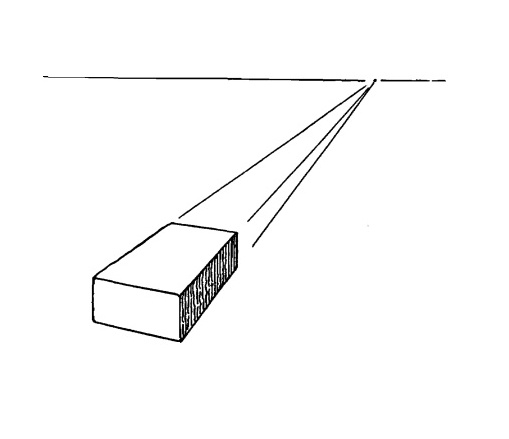
Рис. 5.2.

Определив точку схода и линию уровня глаз, чуть-чуть поверните кирпич.

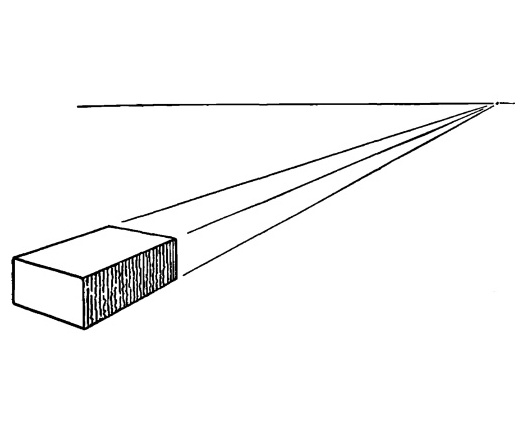
Рис. 5.3.

Это сместит точку схода, но линия уровня глаз останется неизменной. Чем сильнее мы поворачиваем кирпич, тем больше смещается точка схода, но линия уровня глаз всегда остается одной и той же.

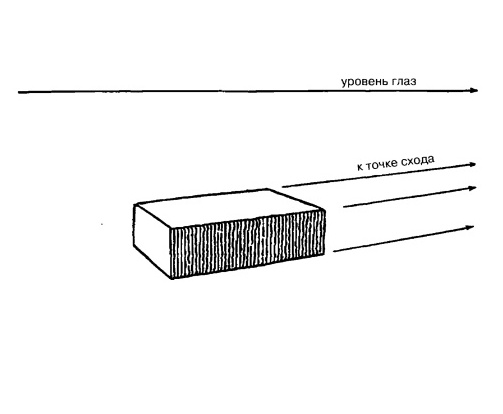
Рис. 5.4.

Но подождите!
Ведь перед нами еще одна группа параллельных линий, изображающих ширину кирпича.

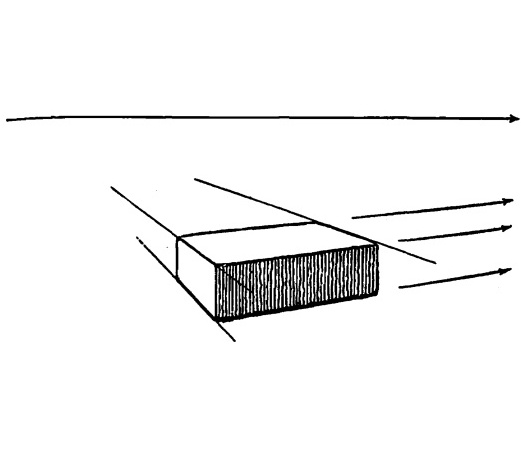
Рис. 5.5.

Давайте продолжим и эти линии. Посмотрим, что нам удастся получить в результате данного опыта.

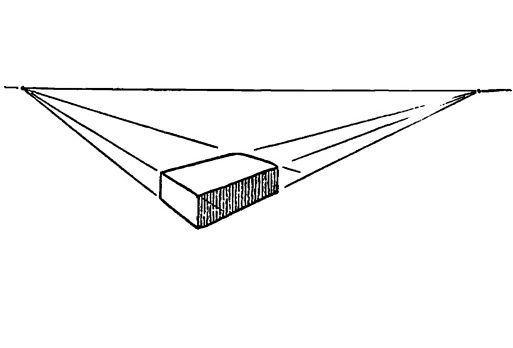
Рис. 5.6. Рисунок кирпича с двумя точками схода.

Вы видите, что кирпич лежит точно так же, как в предыдущем эксперименте, и линии его длины продолжены до точки исчезновения и линии уровня глаз, которая горизонтально проходит через эту точку.

Линии ширины также сходятся в некоей точке, которая лежит на той же самой линии уровня глаз, что и точка схода продолженных линий длины.

Так и должно быть: ведь когда мы смотрим на три стороны кирпича, лежащего на ровной поверхности, уровень наших глаз остается неизменным, вне зависимости от того, обращаем ли мы свое внимание на одну группу параллельных линий или на другую группу.

Линии, параллельные плоскости картины.

Поверните кирпич еще раз в ту или иную сторону, и вы увидите, что первая найденная точка схода смещается вместе с движением кирпича все дальше от него, вдоль линии уровня глаз. Вторая точка схода будет придвигаться все ближе к кирпичу.

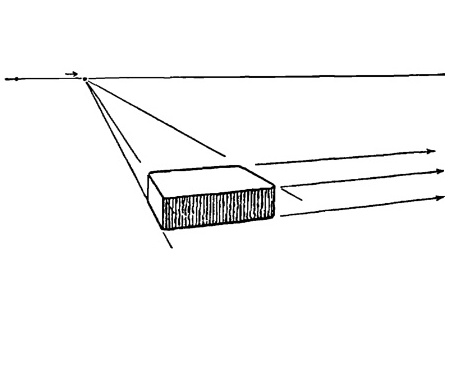
Рис. 5.7.

Когда точка окажется прямо над кирпичом, мы вновь получим подобие рельсового пути с одним набором сходящихся параллельных линий.

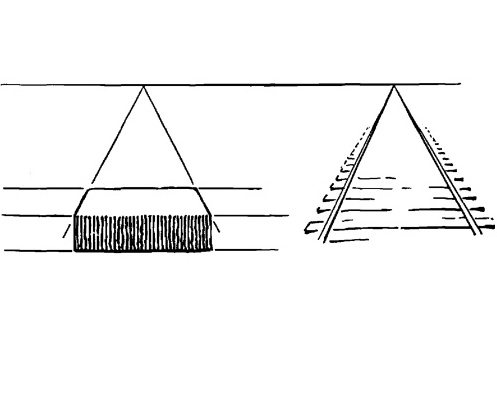
Рис. 5.8.

Другой набор линий теперь будет параллелен горизонту. Эту группу можно также рассматривать, как линии, параллельные плоскости картины, если вы предпочитаете такую точку зрения.

Перпендикулярные линии - линии высоты.

Давайте теперь рассмотрим линии «высоты». Это просто.

Третью группу параллельных линий или линии «высоты» можно нарисовать идущими строго сверху вниз, без наличия точки схода, которую следовало бы учитывать.

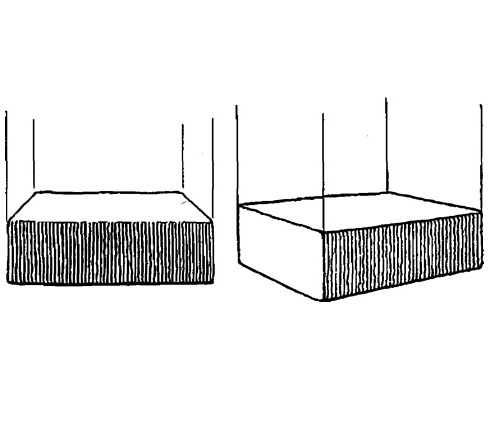
Рис. 5.9.

Это истинно, поскольку линии «высоты» параллельны плоскости картины и ограничены ее пространством. Мы всегда видим только небольшой участок этих линий, вне зависимости от того, как далеко они тянутся вверх или вниз. Линии «высоты» можно сравнить с вертикальными перекладинами рамы того окна, через которое мы смотрим на мир.

Основные выводы пятого урока.

Все параллельные линии, принадлежащие к одной и той же группе рисунка в перспективе, сходятся в одной точке.

Если предмет поворачивать, эта точка будет перемещаться вдоль линии уровня глаз.

Все параллельные линии другой группы сходятся в другой точке.

Обе точки располагаются на линии уровня глаз.

Линии «высоты» идут сверху вниз; точки схода у них нет.

Практические задания и вопросы пятого урока.

1. Нарисуйте книгу, лежащую на столе.
2. Поверните книгу так, чтобы она лежала в ином положении, и снова нарисуйте ее.
3. Отметьте, как располагаются две точки схода всякий раз при изменении положения книги.
4. Поставьте кирпич на торец и зарисуйте его в таком положении. Покажите направление линий «высоты». Сходятся ли они в одной точке?

Рис. 5.10.