Фэн-шуй во всех сферах жизни風水

Учимся рисовать эллипс и цилиндр в перспективе.

Как выглядит цилиндр в перспективе?

Поместим на стол круглую банку из-под кофе и чертежный тубус.

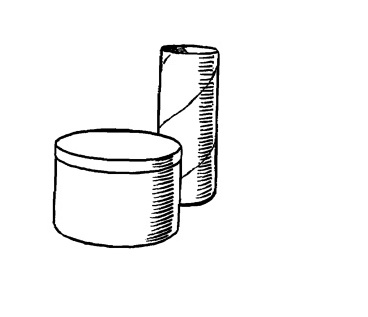
Рис. 13.1.

Это цилиндры.

Верх и дно этих цилиндров представляют собой круги.

Закройте один глаз. Держите эту картинку (картинка на бумаге) правым краем к себе и смотрите на эллипс в направлении, указанном стрелкой. В таком положении эллипс выглядит кругом, а круг кажется эллипсом.

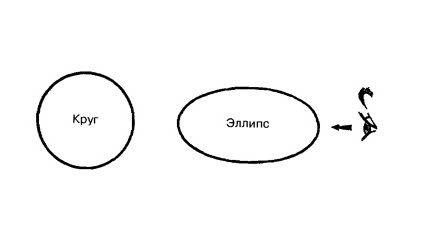
Рис. 13.2.

Так мы обнаруживаем, что, когда мы смотрим на круг сбоку, он выглядит как эллипс.

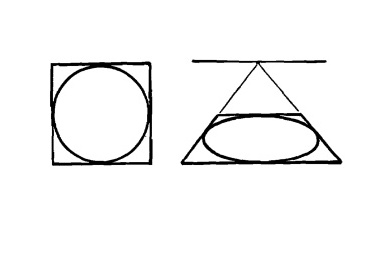
Рис. 13.3.

На иллюстрации вверху показан круг, вписанный в квадрат, и тот же самый круг, вписанный в квадрат, но изображенный в перспективе.

Круг, нарисованный с применением перспективы, превращается в эллипс.

Торцы цилиндра, нарисованного в перспективе, принимают овальную форму.

Рисуем эллипс от руки.

Нарисуйте прямоугольник, длина и ширина которого соответствуют нужным вам длине и ширине эллипса. Эллипс будет касаться контуров прямоугольника в центральной точке каждой из сторон.

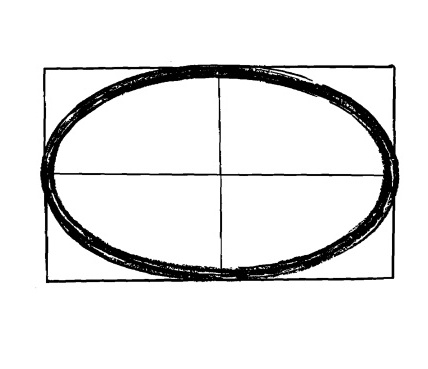
Рис. 13.4.

Попрактикуйтесь рисовать эллипс от руки, используя прямоугольник как основу. Удивительно, как при некоторой практике нарисованный от руки эллипс будет совпадать с тем же самым эллипсом, вычерченным с применением вспомогательных инструментов.

Элементы черчения для начинающих — построение эллипса техническими способами.

Первый способ начертить эллипс.

Давайте начертим эллипс, вписанный в прямоугольник А.

Сначала при помощи циркуля найдите, где круг (показанный на рисунке А) пересекает длинную среднюю линию. Эти пересечения обозначены точками (1) и (2).

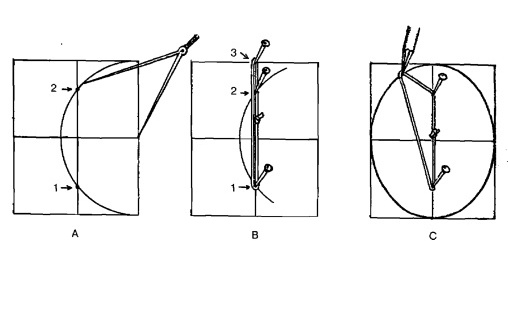
Рис. 13.5.

Воткните в эти точки булавки, а третью булавку (3) — в конце средней линии.

Крепко обвяжите эти булавки прочной льняной ниткой, как показано на рисунке В.

Удалите булавку (3) и очертите карандашом эллипс, как показано на рисунке С.  Нитка должна быть постоянно равномерно натянута.

Второй способ построения.

Вот еще один способ как начертить эллипс, вписанный в прямоугольник А.

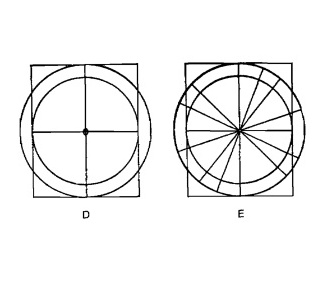
Рис. 13.6.

Начертите два круга с центром в точке О. Диаметр одного круга должен быть равен ширине прямоугольника, а диаметр другого — длине прямоугольника, как показано на рисунке D.

Теперь проведите линии наподобие спиц колеса, как показано на рисунке Е.

Через точки пересечения спиц с малым кругом проведите линии, параллельные длинным сторонам. Через точки пересечения спиц с большим кругом проведите линии, параллельные коротким сторонам.

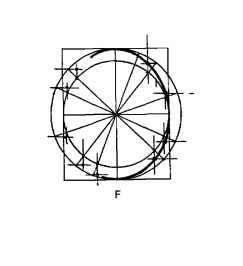
Рис. 13.7.

Эллипс проходит через точки пересечения линий, параллельных коротким сторонам и параллельных длинным сторонам, как показано на рисунке F.

Третий способ построения эллипса.

Приводим еще один способ начертить эллипс определенной величины.

Возьмите полоску бумаги и отметьте на ней половину длины данного в качестве основы прямоугольника. Обозначьте точку буквой L, как показано на рисунке G.

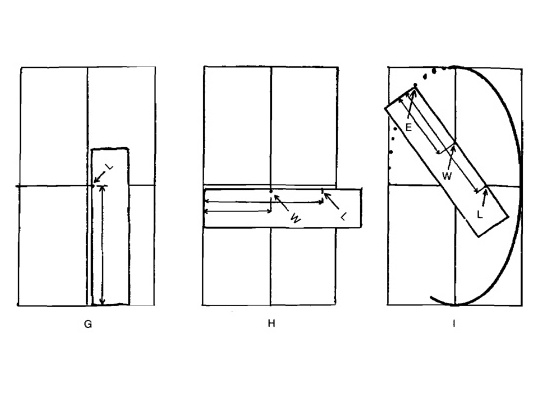
Рис. 13.8.

Далее положите полоску вдоль линии ширины и буквой W обозначьте точку, отмечающую половину этой ширины, как показано на рисунке Н.

Теперь поместите бумажную полоску так, чтобы точка L касалась линии ширины, а точка W касалась линии длины, как показано на рисунке I.

Кончик полоски (обозначенный буквой Е) показывает, где проходит контур эллипса.

Продолжайте двигать полоску по кругу, пока не отметите столько точек, сколько вам нужно.

Этот метод подходит для вычерчивания эллипсов любой величины. При черчении после обозначения точек можно вычертить контур эллипса по лекалу.

Длинные и короткие оси эллипса.

Самая длинная линия, пересекающая эллипс, называется длинной осью.

Самая короткая линия, пересекающая эллипс, называется короткой осью.

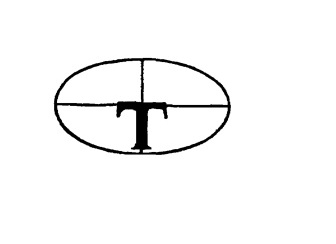
Рис. 13.9.

В месте своего пересечения длинная и короткая оси образуют прямые углы. Будем считать, что длинная ось образует поперечную перекладину буквы T, а короткая ось — ножку буквы T.

Это соотношение между осями и буквой T остается истинным вне зависимости от размера, конфигурации или положения эллипса.

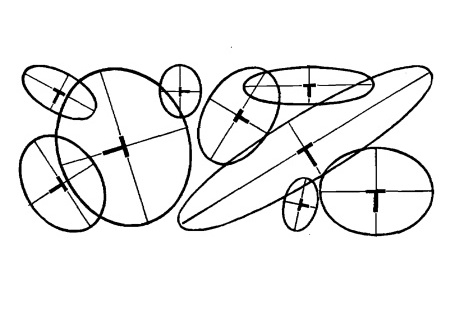
Рис. 13.10.

Построение цилиндра в перспективе, вид сбоку.

Положим один кирпич поверх другого. Предположим, что их торцы образуют квадрат. Нарисуем на торцах диагонали и тем самым найдем центр. Это центр круга, который касается всех четырех сторон квадрата.

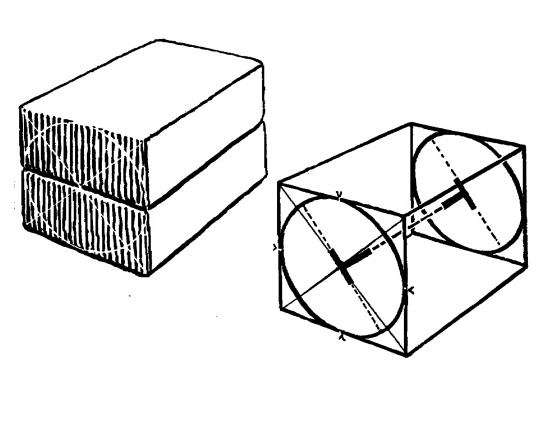
Рис. 13.11. Построение цилиндра в черчении без перспективы.

Этот круг можно расценивать как торец цилиндра, который проходит через всю толщу кирпича. На противоположном торце нарисуем еще один круг.

Линия, проведенная между центрами двух окружностей, — это центральная/осевая линия цилиндра или в нашем случае - ось двух колес. Эта ось — продолжение коротких осей двух эллипсов и ножка двух букв Т.

Длинная ось образует перекладину буквы Т.

Мы начали с предположения, что торцы двух кирпичей, положенных один на другой, образуют квадрат.

Теперь попробуем рисовать цилиндр в перспективе.

Нарисуем кирпичи с применением законов перспективы. Круг, вписанный в квадрат, становится эллипсом, касающимся сторон квадрата (нарисованного в перспективе) в центре каждой из сторон.

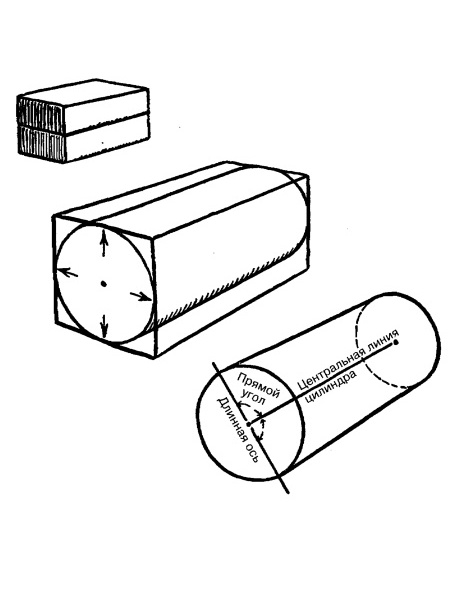
Рис. 13.12. Построение цилиндра в перспективе.

Линия, проведенная через центр круга до точки схода, должна быть центральной линией цилиндра или осью для двух колес.

Линия, проведенная через этот же центр и пересекающая эту ось под прямым углом, будет самой длинной линией или большой осью эллипса.

Большая ось всегда образует прямой угол с центральной осью цилиндра.

Нет никакой разницы, в каком направлении лежит цилиндр и лежит ли он на боку или стоит на торце, большая ось эллипса всегда будет образовывать букву Т с центральной/осевой линией цилиндра. Малая ось эллипса лежит вдоль этой центральной/осевой линии цилиндра. Малая ось эллипса становится центральной линией цилиндра, т.е. они должны совпадать.

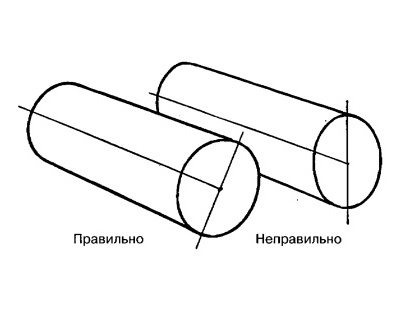
Рис. 13.13. Правильное положение осей эллипса цилиндра в пространстве.

Нарисуйте/начертите цилиндр с соблюдением правил перспективы. Затем поверните бумагу так, чтобы цилиндр оказался в вертикальном положении.

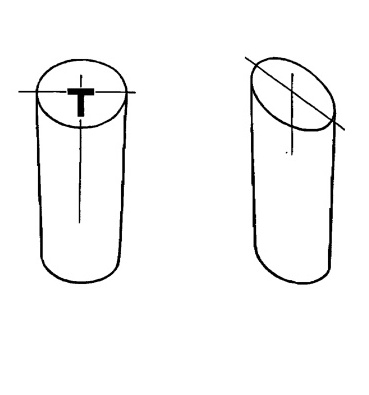
Рис. 13.14. Цилиндр в перспективе в вертикальном положении.

Первое изображение цилиндра является правильным, второе - неправильное.

Рисуем конус, лежащий на боку.

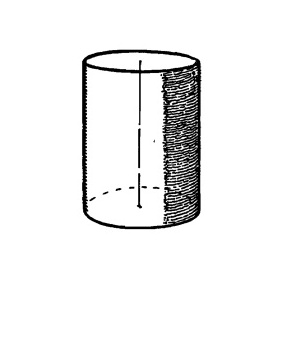
Рис. 13.15.

Конус можно сделать из цилиндра, как показано на рисунке.

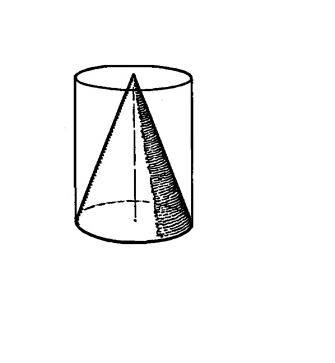
Рис. 13.16.

Теперь мы будем рисовать конус, лежащий на боку.

Сначала рисуем цилиндр, лежащий на боку вдоль черной линии, как показано на рисунке.

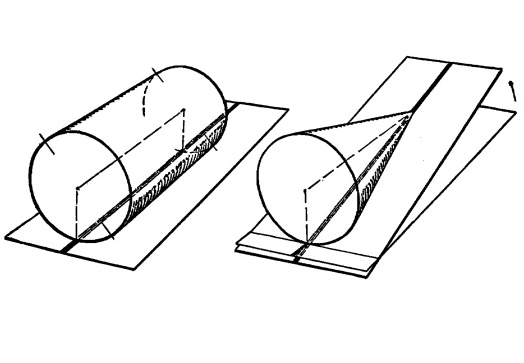
Рис. 13.17.

Затем из цилиндра, лежащего в этом положении, делаем конус.

Мы хотим разместить конус так, чтобы он лежал на плоской поверхности. Чтобы сделать это, мы наклонно приподнимаем поверхность так, чтобы она оказалась прижата к конусу. Верхушка конуса теперь лежит на черной линии.

Теперь давайте расположим всю композицию так, чтобы поверхность снова была горизонтальной, а конус оставался лежать на ней.

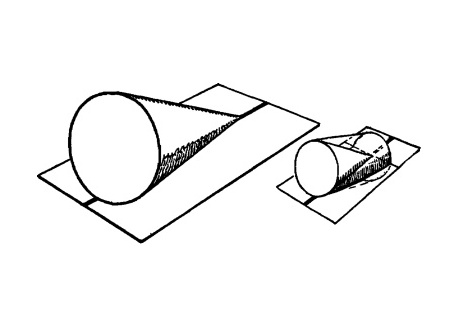
Рис. 13.18.

Таким образом, конус можно считать цилиндром, один торец которого на половину своего диаметра вдавлен в поверхность, на которой он лежит. Затем из этого цилиндра делается конус.

Основные выводы тринадцатого урока.

Круг, нарисованный в перспективе, выглядит как эллипс.

Цилиндр, нарисованный в перспективе, можно рассматривать как два колеса, ось которых образована центральной линией.

Длинная ось эллипса образует перекладину буквы Т с центральной линией.

Практические задания и вопросы тринадцатого урока.

1. Нарисуйте чернильницу. Покажите, что она состоит из цилиндров.
2. Нарисуйте группу кухонных банок для сыпучих продуктов. Теперь положите их набок и зарисуйте в этом положении. Постоянно помните, что вы рисуете цилиндры.
3. Нарисуйте три эллипса с осями 10 на 15 см. Для вычерчивания каждого эллипса используйте один из трех методов, каждый раз разный.
4. Переведите на прозрачную бумагу один из нарисованных вами эллипсов. Положите эту копию поверх других эллипсов. Насколько они совпадают?
5. Нарисуйте лежащие на боку конусы в различных направлениях.

Рис. 13.19.