Фэн-шуй во всех сферах жизни風水

Как найти центр и разделить пространство пополам.

Нахождение центра объекта.

Положите на свой рабочий стол кирпич.

Мелом проведите на поверхности кирпича косые линии из угла в угол. Эти косые линии называются пересекающимися диагоналями.

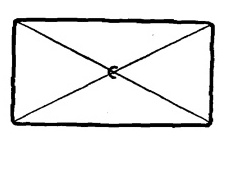
Рис. 12.1.

Эти линии пересекаются в центре поверхности в точке, отмеченной буквой С.

Нарисуйте такие же диагонали на боковых сторонах и торцах кирпича.

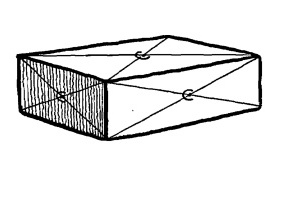
Рис. 12.2.

Нарисуйте кирпич с применением перспективы, показав эти диагонали.

Точка, где они пересекаются, всегда указывается как центр стороны кирпича вне зависимости от его положения.

Сложите пополам листок плотной бумаги и положите его на кирпич.

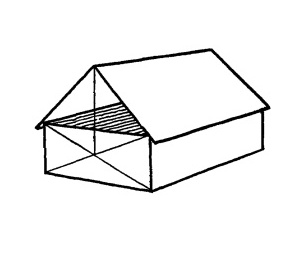
Рис. 12.3.

У вас получился домик. Нарисуйте его с применением законов перспективы.

Край конька крыши находится прямо над точкой пересечения двух диагоналей торца.

В центре торца располагается дверь, а в центре боковой стороны — окно.

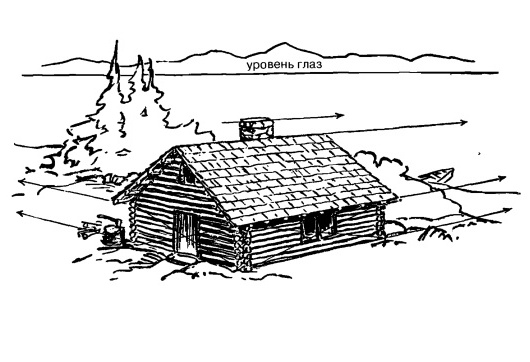
Рис. 12.4.

Их положение определяется пересечением диагоналей.

Использование диагоналей.

Нарисуйте верхнюю часть кирпича, убрав боковые стороны, и покажите диагонали и разделительные линии, идущие к точкам схода.

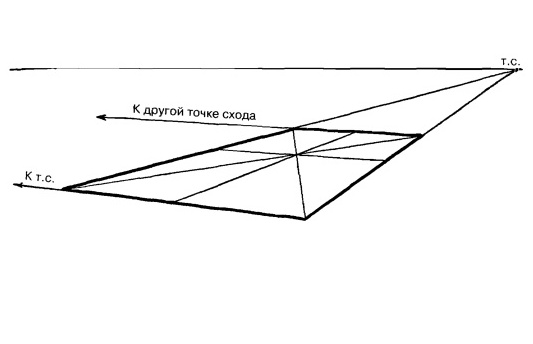
Рис. 12.5.

Прямоугольник или квадрат, поделенный таким образом, находит широкое применение в рисовании.

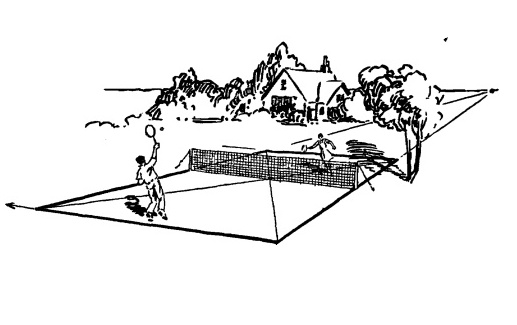
Рис. 12.6.

Верхняя часть кирпича может быть преобразована в теннисный корт.

Или в геометрически правильный сад.

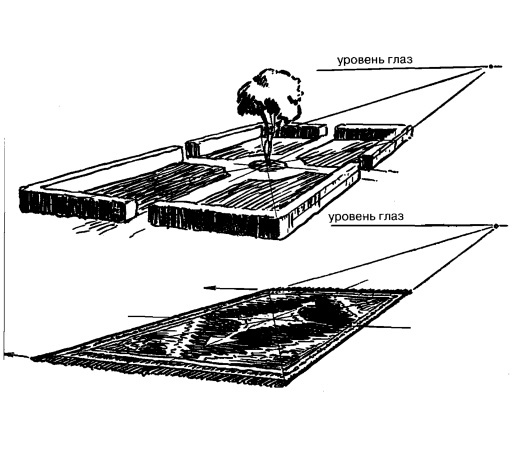
Рис. 12.7.

Или в коврик с узором, или во что угодно, что бы мы ни выбрали. Пересекающиеся диагонали во многом полезны.

Боковая сторона кирпича нарисована в перспективе с диагоналями, пересекающимися в центре.

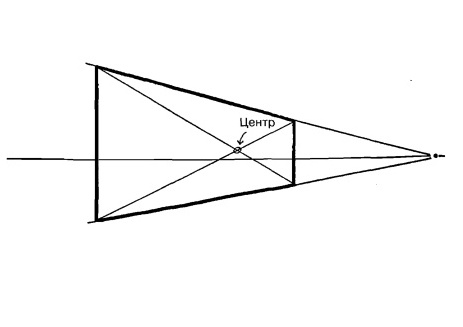
Рис. 12.8.

Боковая сторона кирпича может быть преобразована в стену здания, а диагонали отмечают положение двери в центре.

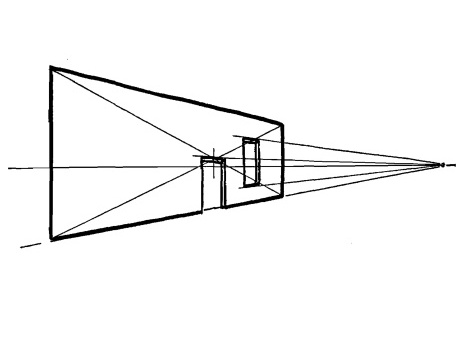
Рис. 12.9.

Боковую сторону кирпича можно преобразовать в афишу или во что угодно, что бы мы ни выбрали. Мы поймем, что диагонали могут быть полезны во многих отношениях.

Рис. 12.10.

Рисуя афишу, отметьте, что центр в перспективе располагается несколько правее центра рисунка, который можно найти путем измерения.

На верхней части кирпича нарисованы диагонали. Линии, проведенные через центр к точкам схода, делят кирпич пополам.

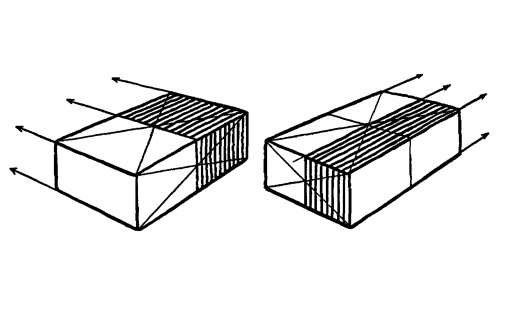
Рис. 12.11.

Кирпич с нарисованными на нем диагоналями можно использовать в качестве основы для большого количества рисунков с применением законов перспективы.

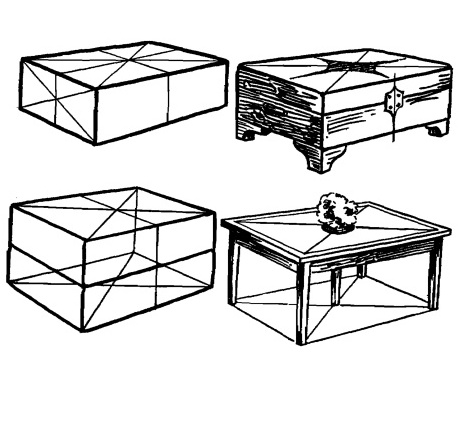
Рис. 12.12.

Нахождение расстояния в перспективе, используя диагонали.

Перед нами два столбика одной и той же высоты.

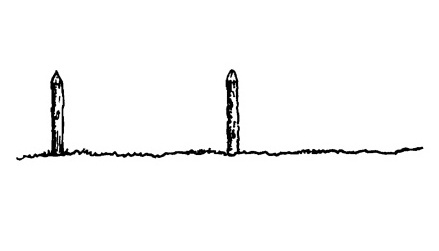
Рис. 12.13.

Теперь нарисуем три параллельные линии: одну по верху, одну по центру и одну у основания столбиков.

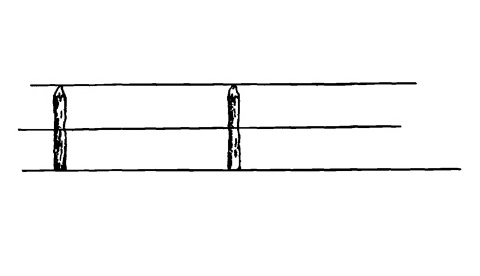
Рис. 12.14.

Теперь, если мы проведем линию через верх первого столбика и через центр второго столбика, то мы обнаружим, что она пересекает линию основания там, где должен располагаться третий столбик.

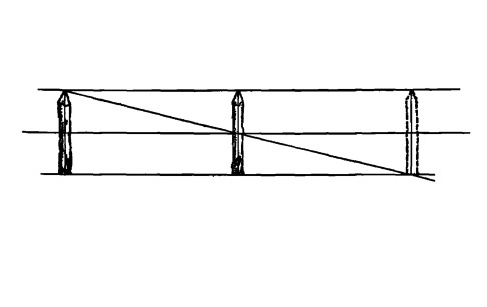
Рис. 12.15.

Это способ применения диагоналей, использованный другим путем. В этом случае мы используем его для того, чтобы найти четвертую сторону поверхности кирпича при условии, что у нас есть три стороны и центральные линии.

Те же самые соотношения будут верны, если мы нарисуем ряд столбиков с соблюдением законов перспективы. Разместив два столбика, мы сможем нарисовать их столько, сколько нужно, — и расстояние между ними будет соблюдено.

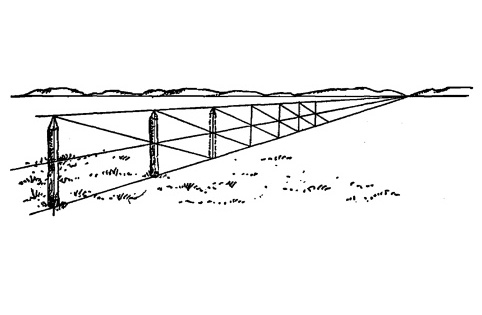
Рис. 12.16.

Это правило также истинно, когда разделительные линии проходят параллельно плоскости картины, как в случае, когда мы рисуем блоки фундамента или колонну грузовых машин. В этом случае разделительные линии сходятся к другим точкам схода. На рисунке эти линии представлены столбиками ограды.

Основные выводы двенадцатого урока.

Диагонали применяются для нахождения центра прямоугольной поверхности, вне зависимости от того, нарисована эта поверхность в перспективе или нет.

Кирпич с нарисованными на нем диагоналями может быть использован в качестве основы для большого количества рисунков в перспективе.

Если на рисунке помещены два объекта одной и той же высоты, мы можем добавить их столько, сколько нужно, и расстояние между ними будет соблюдено.

Пересекающимися диагоналями называются косые линии, проведенные из угла в угол.

Практические задания и вопросы двенадцатого урока.

1. Нарисуйте стол в перспективе. Теперь поместите точно в его центре вазу с цветами.
2. Сливное отверстие находится в центре прямоугольной ванны. Изобразите это на рисунке с применением законов перспективы.
3. В торцевой стене комнаты есть окно. Переплет делит окно на четыре части. Изобразите это в сходящейся перспективе. Изобразите это в перспективе с двумя точками схода.
4. Нарисуйте ряд деревьев разной высоты, растущих на равном расстоянии друг от друга. (Подсказка: наметьте положение деревьев так, как если бы это были столбики. Затем пририсуйте к ним листву различной высоты.)
5. Тротуар выложен черными и серыми плитами, чередующимися через одну. Нарисуйте этот тротуар.
6. Колонна грузовиков едет по равнине. Нарисуйте эту колонну.

Рис. 12.17.