Фэн-шуй во всех сферах жизни風水

Разделим поверхность в перспективе и изобразим шахматную доску.

Начнем с разделения поверхности.

Проведите горизонтальную линию, разделяющую поверхность кирпича на три равные части.

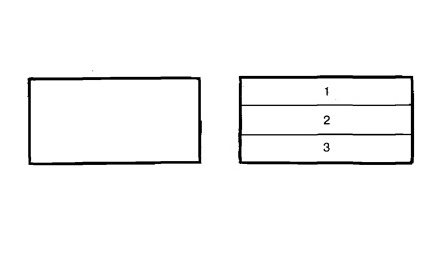
Рис. 15.1.

Теперь проведите линию из угла в угол. В точках пересечения линий нарисуйте вертикальные линии.
Эти линии так же делят кирпич на три части, но не по горизонтали, а по вертикали.

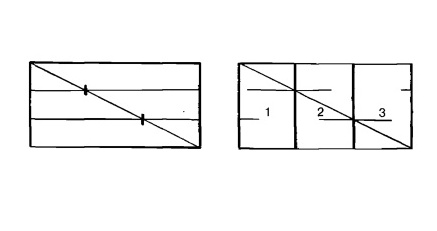
Рис. 15.2.

Это правило верно для разделения на четыре равные части или на пять равных частей, в общем, на столько частей, на сколько мы захотим поделить.

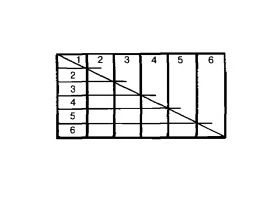
Рис. 15.3.

Разделение поверхности в перспективе.

Если кирпич нарисован с соблюдением законов перспективы, то метод разделения, описанный в первой части этого урока, по-прежнему правилен.

Расположение вертикальных разделительных линий находится согласно законам перспективы.

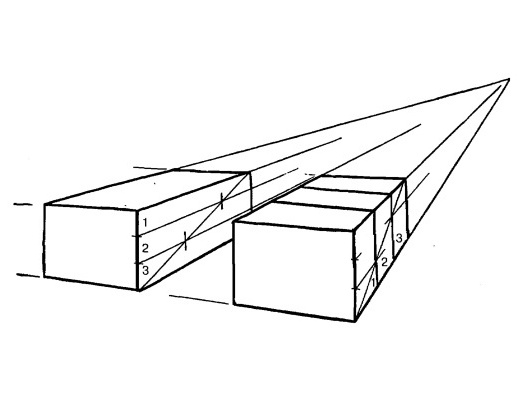
Рис. 15.4.

Этот метод верен для такого количества разделений, какое вы захотите сделать.

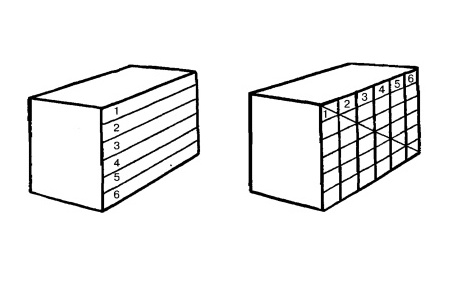
Рис. 15.5.

Построение окон и колонн здания в перспективе.

Давайте нарисуем здание с восемью рядами окон, расположенных через равные промежутки.

Сначала разделим угловую линию на восемь равных частей.

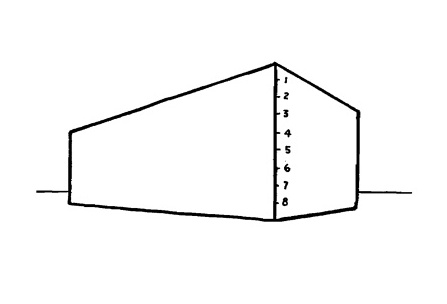
Рис. 15.6.

Проведем от этих точек линии до точки схода здания. Линия от угла до угла (как та, что мы проводили на кирпиче) поделит стену на восемь равных частей.

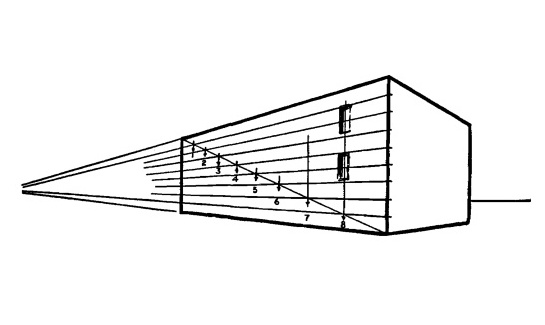
Рис. 15.7.

Таким образом мы наметим центральные линии окон так, как они должны выглядеть в перспективе. Этот метод может быть использован для создания на рисунке ряда колонн, контрфорсов, панелей, деревьев или в любом другом случае, когда необходимо поделить некий отрезок на равные части.

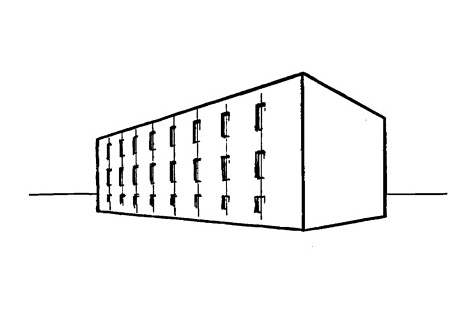
Рис. 15.8.

Шахматная доска в сходящейся перспективе.

При рисовании шахматной доски в сходящейся перспективе сначала нужно поделить ближнюю или дальнюю сторону на восемь равных частей.

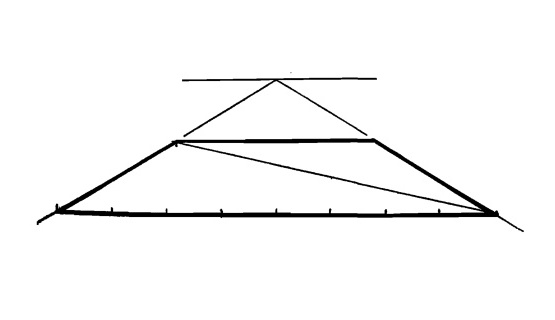
Рис. 15.9.

Линии, идущие к точке схода, поделят доску на восемь частей.

Пересечем все эти линии диагональю.

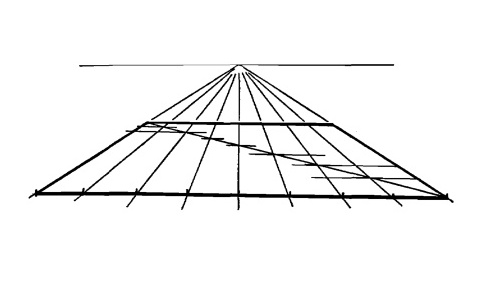
Рис. 15.10.

Из точек пересечения разделительных линий с диагональю проведем горизонтальные линии. Тем самым мы получим клеточки шахматной доски, нарисованные в соответствии с законами перспективы.

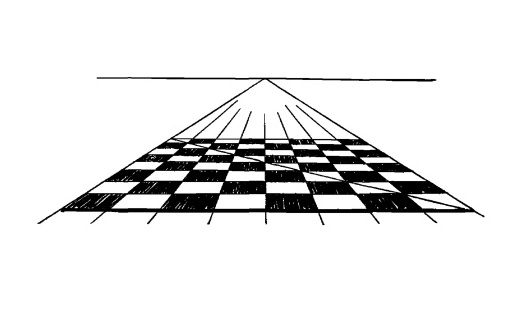
Рис. 15.11.

Шахматная доска в перспективе с двумя точками схода.

В случае с шахматной доской, нарисованной в перспективе с двумя точками схода, нам нужно рассмотреть две стороны доски, причем обе стремятся к своей точке схода.

Если мы хотим нарисовать шахматную доску в таком плане, давайте рассматривать ее как верхнюю сторону коробки.

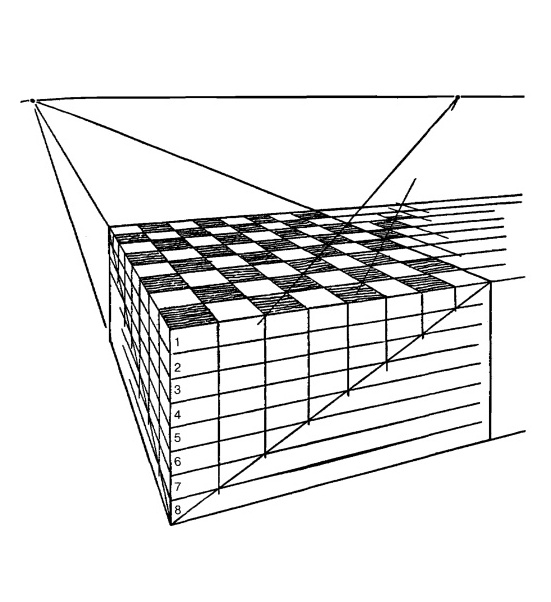
Рис. 15.12.

Теперь мы используем тот же самый метод, который применяли к зданию, и поделим каждую из сторон коробки на восемь равных частей.

Теперь продолжим вертикальные линии через верхнюю сторону коробки до точек схода. Эти линии образуют клеточки шахматной доски в соответствии с законами перспективы.

Нарисованный участок можно увеличить, проведя косую линию через ряд клеточек за пределы доски. Этот метод показан на схеме.

Если рисунок выполнен правильно, то косые линии встретятся в новых точках схода на линии видимого горизонта.

Этот «шахматный» метод используется при рисовании квадратов линолеума и выложенного плитками пола, узоров на ковре и потолочных панелей.

Для изображения потолка рисунок нужно перевернуть.

Рисунок в перспективе с различными промежутками.

Если окна в здании разделены промежутками разной длины, можно использовать способ с диагоналями точно так же, как при наличии равных промежутков.

Возьмите полоску бумаги и отметьте расположение дверей и окон, используя в качестве единицы измерения высоту здания.

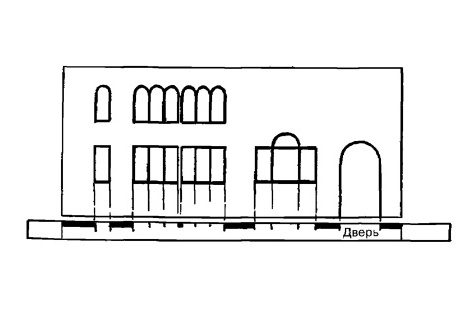
Рис. 15.13.

Нарисуйте здание так, чтобы высота ближайшего к вам угла была такой же, как длина мерной полоски.

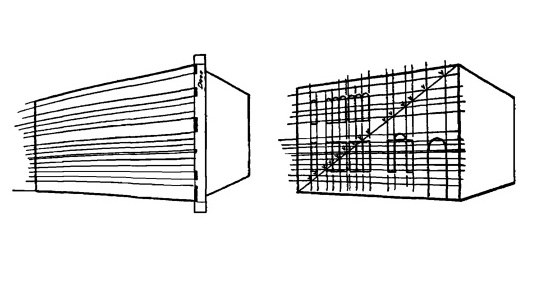
Рис. 15.14.

Отметьте на этом углу нанесенные на полоску промежутки и проведите от этих отметок линии до точки схода этой стороны здания. Пересечение этих линий с диагональю даст нужные промежутки между окнами и дверьми.

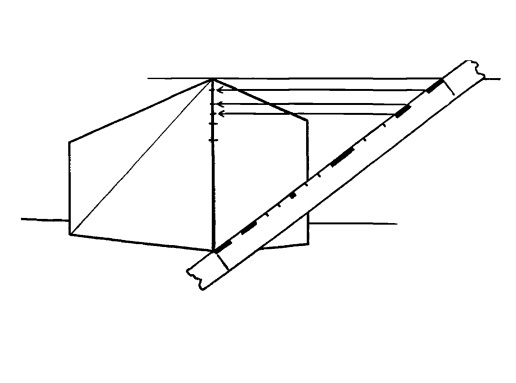
Рис. 15.15.

При желании здание можно нарисовать меньше. При этом мерную полоску вовсе не нужно уменьшать в соответствии с уменьшением рисунка.

Нарисуйте здание нужного размера, затем проведите горизонтальную линию от его верхнего угла и положите мерную полоску между этой линией и нижним углом здания, как показано на рисунке.
После этого горизонтальными линиями перенесите отмеренные на бумаге промежутки на линию угла здания.

Рис. 15.16. Готовое здание

Существование других способов разметки.

Еще один метод, используемый для разметки промежутков, будет показан в конце двадцатой части.

Существует много способов, используемых для разметки неравномерных промежутков на рисунке в перспективе. Здесь они не приводятся, но их можно найти в учебниках по рисованию и черчению в перспективе. Метод, приведенный здесь, прост, практичен и легко запоминается.

Основные выводы пятнадцатого урока.

Поверхность, поделенная в одном направлении, может быть точно так же поделена в другом направлении путем использования диагонали. Этот диагональный метод крайне полезен.

Если разделение происходит при наличии неравномерных промежутков, этот метод все равно применим.

Практические задания и вопросы пятнадцатого урока.

1. Поделите на десять частей две вертикальные стороны кирпича, изображенного в перспективе. Теперь поделите его верхнюю сторону на сто равных частей.
2. Нарисуйте здание с применением законов перспективы. Нарисуйте восемь рядов окон на одной стороне и шесть на другой.
3. Нарисуйте шахматную доску в перспективе с двумя точками схода. Покажите, что диагонали сходятся в точке на уровне глаз.
4. Нарисуйте боковую стену дома с дверью и двумя окнами. Теперь нарисуйте этот дом в перспективе. Изобразите одно окно в центре торцевой стены.
5. Нарисуйте античный храм с колоннами.

Рис. 15.17.